The sample variance is the mean of the square of the deviations of each measurement from the mean (called mean square deviation).

Enter x_i values: (hit Autofill and Plot) to see the sample variance s² and sample standard deviation s. 

The sum of deviations å(x_i - )= 0 is expected, since it follows that 
åx_i = N, i.e.  .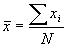

which is the definition of .

Most points (approx 2/3) lie within ± s of the mean .

N must be at least 2, since we cannot estimate a spread in values from a single measurement.

s is an estimate of s, the standard deviation of a single measurement. It is not an estimate of s(), the standard deviation of the mean ... next.