Suppose we have a set of measurements of n quantities, x_i (i = 1 to n) each with a standard deviation s_i, and true mean m_i. We can calculate a quantity called chi-squared, defined as  . 

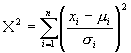We will look at a simple example. Here the  measurements are of the same quantity, i.e. a single parameter, so m_i = m independent of x_i . Therefore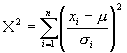

See how C² varies with assumed value for m: Vary the value on the x_i plot (up or down).

Find m for the minimum C², it should equal the weighted mean.