|
A full plot of C2 versus m
shows a minimum: C2min
at m = mmin.
In the example,
mminis
the weighted mean of the measurements obtained by minimizing C2,
i.e. determining the 'least-squares' (best fit) value. 
Use the mouse (LHB) and move the purple square to find the
uncertainty in mmin (e
= m - mmin) obtained
from m when C2
= C2min +1. It should
be close to 'Error(calc)', which is obtained from the formula:  .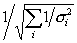
Hit
'reset' to get a new set of values. |
